CGMM | Rotation in 2D Plane | Exp - 9

Rotation in 2D Plane

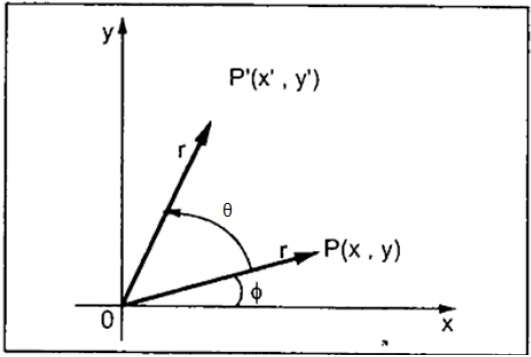
In rotation, we rotate the object at particular angle θ (theta) from its origin. From the following figure, we can see that the point P(X, Y) is located at angle φ from the horizontal X coordinate with distance r from the origin.

Let us suppose you want to rotate it at the angle θ. After rotating it to a new location, you will get a new point P’ (X’, Y’).

Using standard trigonometric the original coordinate of point P(X, Y) can be represented as −

X=rcosϕ......(1)

Y=rsinϕ......(2)

Same way we can represent the point P’ (X’, Y’) as −

x′=rcos(ϕ+θ)=rcosϕcosθ−rsinϕsinθ.......(3)

y′=rsin(ϕ+θ)=rcosϕsinθ+rsinϕcosθ.......(4)

Substituting equation (1) & (2) in (3) & (4) respectively, we will get

x′=xcosθ−ysinθ

y′=xsinθ+ycosθ

Representing the above equation in matrix form,

[X′Y′]=[XY][cosθ−sinθsinθcosθ]   OR$$<br>$$$$[X^{\prime }{Y}^{\prime }]=[XY]\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]OR$$

P’ = P . R

Where R is the rotation matrix

R=[cosθ−sinθsinθcosθ]$$\mathrm{<br>}$$$$R=\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]$$$$<br>$$

The rotation angle can be positive and negative.

For positive rotation angle, we can use the above rotation matrix. However, for negative angle rotation, the matrix will change as shown below −

R=[cos(−θ)−sin(−θ)sin(−θ)cos(−θ)]$$\mathrm{<br>}$$$$R=\left[\begin{array}{cc}cos(-\theta )& sin(-\theta )\\ -sin(-\theta )& cos(-\theta )\end{array}\right]$$$$<br>$$

=[cosθsinθ−sinθcosθ](∵cos(−θ)=cosθandsin(−θ)=−sinθ)

For more info visit tutorialspoint

Problem Statement

Rotate any object in the 2D plane by an angle of 180o.

File: Download here